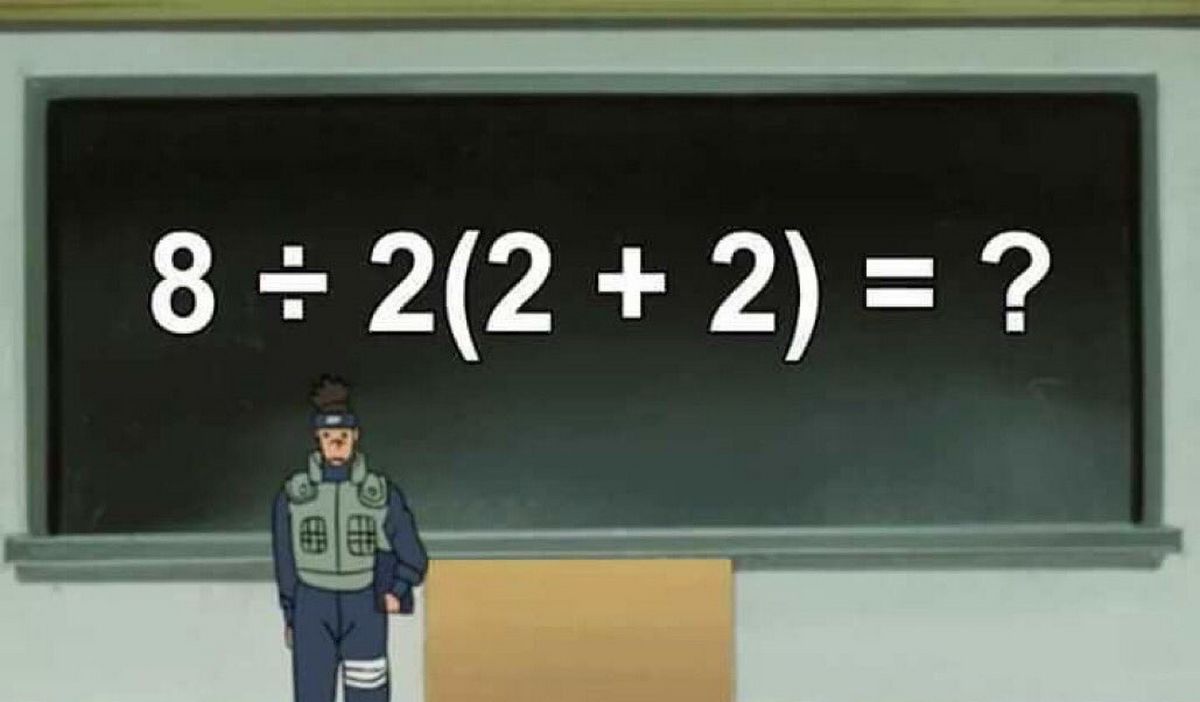[ad_1]
A simple mathematical operation that generates consensus at the local level has caused a battle of knowledge on the Internet.
in an old math exercise whose fame is revived every so often in networks, because there is no consensus about your result. The mathematical operation 8/2(2+2) attack again. How is it solved correctly?
It is a simple mathematical operation that apparently has no difficulty. 8/2(2+2) It’s a primary exercise. But there are people who say that the result is 1others that it is 16… and some more. Who has the reason?
In school we were taught that the order of operations is parentheses, powers and roots, multiplication and division, addition and subtraction, from left to right. With multiplication and division, and addition and subtraction, other things being equal:

If we apply these rules, we have:
- 8/2(2+2), that is, 8/2*(2+2)
- 8/2*(4)
- 4*(4)
- 16
He result is 16. Easy, right? Well it is not too much…
If it’s so simple, then… why is there graduates in Mathematics they say that the result is 1?
The reason is that in Spain and most countries, it is used the PEMDAS orderexplained above: Parentheses, Powers and roots, Multiplication and Division, Addition and Subtraction.
But in some places it is taught the BODMAS orderthat gives precedence to operations where any parentheses are involved. That is, first you have to remove the parentheses. If we apply this order:
- 8/2(2+2), that is, 8/2*(2+2)
- 8/2*(4)
- 8/8
- 1
result is 1.
Who has the reason? Well, according to the University of Berkeley… both results are fine. The problem is that the operation is poorly formulated, it is ambiguous. When there is ambiguity, more parentheses must be added.
If the person who wrote the formula wants you to the result is 1 must write 8/(2(2+2)). And if you want it to be 16then the operation is (8/2)(2+2). In this way there is no room for mistakes, use the order PEMDAS or BODMAS.
A Math operation, 8/2(2+2)continues to generate debate on the Internet, because it gives rise to different resultsdepending on who you ask. But it has a unique solution… if you reformulate it correctly.
[ad_2]